2019-12-01

了解 SIMD 指令

SIMD 是一种常见的利用单指令完成多数据量处理的计算方式。本文作为 SIMD 文章的引子，先来了解简单的 SIMD 使用和概念。

SIMD 的含义

SIMD 的全称是 Single Instruction Multiple Data。简要来说，就是通过一条指令完成多条数据处理的行为。我们知道，虽然程序是由一条条机器指令组成，但是实际上执行一条机器码包含了多个过程，包含取指令、分析指令到执行等，如下图所示（暂时先忽略流水线并行）

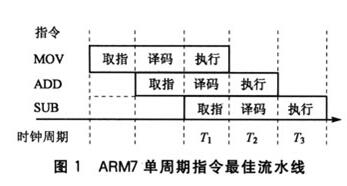
而在这其中，每一个阶段，都会消耗一个或多个机器周期。如果我们认为，取指令和分析指令（译码）可以近似的认为是一个机器周期内完成，那么不同的指令，在执行阶段耗费的机器周期则大不相同。

举个例子，可能加法指令的执行阶段需要两个机器周期；而乘法可能需要5-6个机器周期。那么，当我们无法缩短指令的执行周期缩短的时候，利用 SIMD 技术，则可以在相同的执行周期内完成更多的数据处理，这样也同等的提升了单位时间内的数据吞吐，提高了计算性能。

在 Intel 的手册上，提供了包含 MMX, SSE, AVX 等系列的并行指令，面向不同长度的数据并行，比如：

MMX 并行计算 64bit 的数据。
SSE 并行计算 128bit 的数据。
AVX 并行计算 256bit 的数据。
AVX512 并行计算 512bit 的数据。

更多详细的使用可以参考：

Intel 手册

SIMD 的使用方式

由于绝大多数的人对 SIMD 还不甚了解，因此本文基于大家比较熟悉的环境 Xcode + x86/64 架构来完成。

主要是我懒，不想再翻 ARM 的手册了。

这里我们以一个简单的 256bit (32 byte) 加法改写成 SIMD 的形式来验证：

原始版本：

double input1[k] = {1, 2, 3, 4};
double input2[k] = {5, 6, 7, 8};
double result[k] = {0};

for (int i = 0; i < k; i++) {
    result[i] = input1[i] + input2[i];
}

SIMD 版本：

const int k = 4;
double input1[k] = {1, 2, 3, 4};
double input2[k] = {5, 6, 7, 8};
double result[k] = {0};

__m256d a = _mm256_load_pd(input1);
__m256d b = _mm256_load_pd(input2);

__m256d c = _mm256_add_pd(a, b);
_mm256_store_pd(result, c);

原始版本比较好懂，我们主要来深入看下 SIMD 中代码的意思：

_mm256_load_pd 就是从内存中读取一个地址，这个地址返回为 __m256d 的向量（256bit）。其中， __mm256d的定义为下：
```
typedef double __m256d __attribute__((__vector_size__(32)));
```
这个含义的意思就是 __m256d 的长度是 32 byte（256bit），而这个 32 byte 是按照 4 个 double 元素构成的。
_mm256_add_pd 就是对两个 256bit 的向量元素进行直接相加。
_mm256_store_pd 就是 _mm256_load_pd的逆运算，不再赘述。

注意：如果提示需要 AVX 支持的话，请在 Xcode 对应的代码文件处添加 Compiler Flag: -mavx

用 SIMD 实现求和加法

既然说了 SIMD 的本质还是为了提升单位时间内的计算吞吐量，我们还是用一个简单的例子，加法求和来实践一下：

常规的代码如下：

double CommonAdd(double *data, int count)
{
    double result = 0;

    for (int i = 0 ; i < count; i++) {
        result += data[i];
    }

    return result;
}

SIMD 的代码如下：

double AVXAdd(double *data, int count)
{
    int offset = 0;

    __m256d v1;
    __m256d sum = _mm256_setzero_pd();

    double ret = 0;

    for (int i = 0; i < count/4; i++) {
        v1 = _mm256_load_pd(data + offset);
        sum = _mm256_add_pd(sum, v1);
        offset += 4;
    }

    sum = _mm256_hadd_pd(sum, sum); // 水平求和

    ret += sum[0];
    ret += sum[2];

    return ret;
}

测试代码如下：

int main() {

    struct  timeval   start;
    struct  timeval   end;


    const int k = 512 * 512;

    const int loop = 1;

    double input1[k];

    for (int i = 0; i < k; i++) {
        input1[i] = i;
    }

    gettimeofday(&start, nullptr);

    for (int j = 0; j < loop; j++) {
        CommonAdd(input1, k);
    }

    gettimeofday(&end, nullptr);

    printf("tv_sec:%ld\n",end.tv_sec - start.tv_sec);
    printf("tv_usec:%d\n", end.tv_usec - start.tv_usec);

    std::cout << " ======================= " << std::endl;

    gettimeofday(&start, nullptr);

    for (int j = 0; j < loop; j++) {
        AVXAdd(input1, k);
    }

    gettimeofday(&end, nullptr);

    printf("tv_sec:%ld\n",end.tv_sec - start.tv_sec);
    printf("tv_usec:%d\n", end.tv_usec - start.tv_usec);

    return 0;
}

这里，我们选择了图像处理里面比较常见的 512 * 512 大小来做验证，在我的 2015款 MacBookPro 上可以得到大致如下两个性能耗时：

常规方法【774 us】
SIMD 【560 us】

别小看这一点的性能差距，对于大运算量的端侧深度学习可就有很显著的差距了。

后记

本文只是仅仅介绍了最常规的 SIMD 使用方式。但是在实际设计的过程中，不可能像我们这么简单的去应用。随之而来的，你会发现伴随着许多不同的坑，包含不规范的应用导致性能的下降和崩溃问题。这些都会留在后面我们去解决。